

A main question we investigate is how robots can interact with their surroundings, and learn by trial and error. Reinforcement Learning (RL) is the mathematical framework to study such behavior, and this video gives a brief exposition to RL research in our lab.

A robot needs a model of the world to plan its course of action. A straightforward tool for this is classical mechanics. However, it turns out that the equations of motion for robot interaction with complex objects (think, for example, of a cloth or a rope) is too difficult. An alternative method aims to learn models of the world, by learning to predict how the world will change once the robot interacts with it. This video gives a brief exposition to world models research in our lab.

A robot needs a model of the world to plan its course of action. A straightforward tool for this is classical mechanics. However, it turns out that the equations of motion for robot interaction with complex objects (think, for example, of a cloth or a rope) is too difficult. An alternative method aims to learn models of the world, by learning to predict how the world will change once the robot interacts with it. This video gives a brief exposition to world models research in our lab.


The generalization problem in RL is how to train a policy on a set of training tasks to solve an unseen (but similar) test task. The challenge is that all RL algorithms strongly overfit. In this work we discovered that learning Maximum-Entropy exploration generalizes better than learning to maximize reward. We use this to set a new SOTA for the ProcGen benchmark.

The generalization problem in RL is how to train a policy on a set of training tasks to solve an unseen (but similar) test task. The challenge is that all RL algorithms strongly overfit. In this work we discovered that learning Maximum-Entropy exploration generalizes better than learning to maximize reward. We use this to set a new SOTA for the ProcGen benchmark + significantly improve on hard games like Maze and Heist.


The generalization problem in RL is how to train a policy on a set of training tasks to solve an unseen (but similar) test task. The challenge is that all RL algorithms strongly overfit. In this work we discovered that learning Maximum-Entropy exploration generalizes better than learning to maximize reward. We use this to set a new SOTA for the ProcGen benchmark + significantly improve on hard games like Maze and Heist.

The generalization problem in RL is how to train a policy on a set of training tasks to solve an unseen (but similar) test task. The challenge is that all RL algorithms strongly overfit. In this work we discovered that learning Maximum-Entropy exploration generalizes better than learning to maximize reward. We use this to set a new SOTA for the ProcGen benchmark + significantly improve on hard games like Maze and Heist.
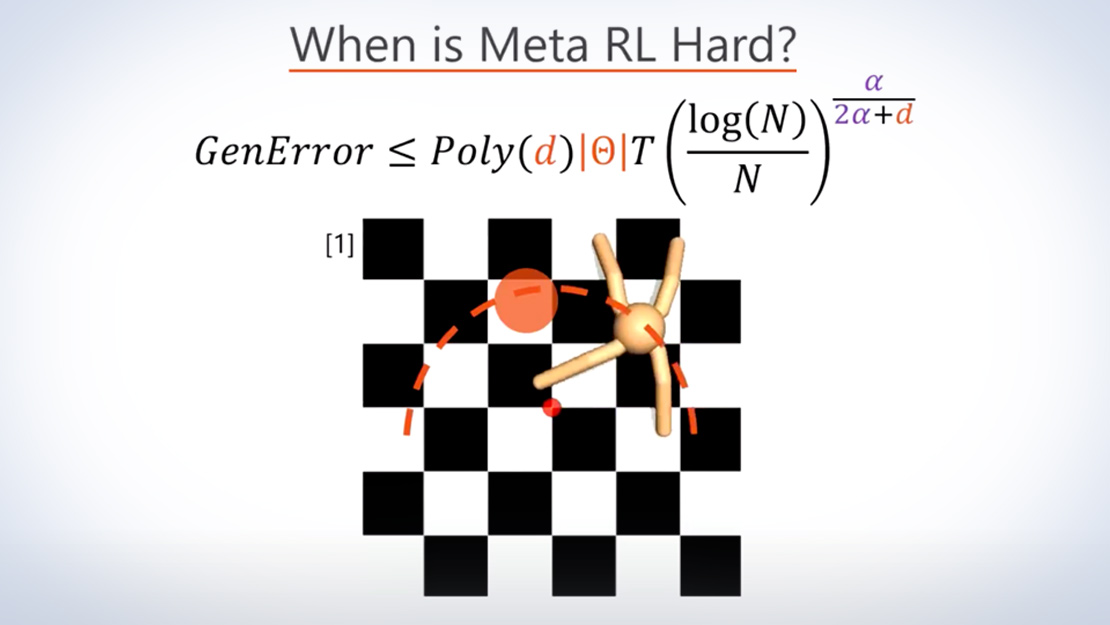
In meta reinforcement learning (meta RL), an agent learns from a set of training tasks how to quickly solve a new task. The optimal meta RL policy is well defined, and here we explore how many training tasks are required to guarantee approximately optimal behavior with high probability. Key in our approach is using the implicit regularization of kernel density estimation methods, which we use to estimate the task distribution. We further demonstrate that this regularization is useful in practice, when `plugged in’ the state-of-the-art VariBAD meta RL algorithm



